Jack owns a paint shop. As business had been rather bad lately, he decided to clear his older stock by holding a promotion, where customers get to buy 3 cans of paint for the price of 2. He decided to package these cans of paint in a promotion box, which has a square base area. The cans of paint are perfectly cylindrical in shape and the diameters of the tin lids are all 10cm. He was pondering over how he should best fit the cans of paint in a square base box such that he would minimize the materials used for the box.
"How about this arrangement?" His friend suggested, "We just need a 20cm by 20cm square base box."
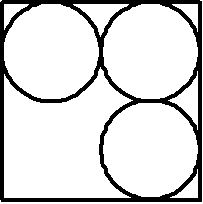
Jack gasped at the gaping hole in this arrangement. What a waste of space! Surely, there was a better arrangement to place 3 cylinders in a square base box?
To the nearest 0.01cm, what is the side length of the smallest square base that can fit the 3 cans of paint?
If you know the answer, post it in the comments section of this post.
If you know the answer, post it in the comments section of this post.
hint: try drawing a diagram of the square that best fits the 3 circles. the new side length is not very far off from 20 (:
ReplyDeletehaha. it appears that this puzzle is rather difficult? to solve this puzzle you should try drawing out how you can best pack the 3 circles. (by pushing them a teeeny weeny bit closer?)
ReplyDeleteeven if it doesnt seem to differ alot, it doesnt matter, just go with your intuition. Then try calculating the side length to see if it is indeed smaller.
18.6?
ReplyDeleteSorry 18.66 :)
ReplyDeletecorrect solution is posted
ReplyDelete