Chork's Puzzle 31
Difficulty Rating: 6
Part 2 of the square-circle-triangle trilogy
Haven't had enough of squares circles and triangles? This is the 2nd of 3 puzzles featuring these three cool shapes!
Chork drew a square, a circle and an equiltateral triangle of equal perimeters. The square and triangle both intersect the circle but do not intersect each other (as shown in the figure below).
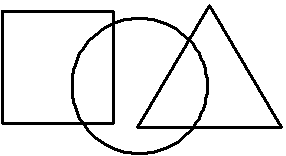
The shapes intersect in such a way that the area enclosed but the square only, the area enclosed by the circle only and the area enclosed by the triangle only are all equal. Given that the area of the INTERSECTION of the circle and the square is 2006,
Part 2 of the square-circle-triangle trilogy
Haven't had enough of squares circles and triangles? This is the 2nd of 3 puzzles featuring these three cool shapes!
Chork drew a square, a circle and an equiltateral triangle of equal perimeters. The square and triangle both intersect the circle but do not intersect each other (as shown in the figure below).
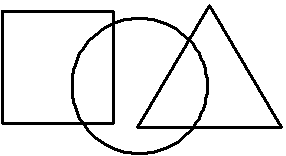
The shapes intersect in such a way that the area enclosed but the square only, the area enclosed by the circle only and the area enclosed by the triangle only are all equal. Given that the area of the INTERSECTION of the circle and the square is 2006,
What is the common perimeter of the 3 shapes?
If you know the answer, post it in the comments section of this post.
If you know the answer, post it in the comments section of this post.


