Chork's Puzzle 32
Difficulty Rating: 5
Part 3 of the square-circle-triangle trilogy
The last puzzle of the set of 3 square-circle-triangle puzzles! (: Unfortunately you won't see much of the trio in future puzzles anymore!
Inscribed in a square is a circle, as shown below:
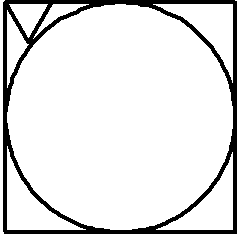
Suppose an equilateral triangle is fitted into one of the space bounded by the circumference of the circle and the sides of the square, such that one vertice of the triangle touches a corner of the square, and the other vertice just touches the circumference of the circle. (Diagram above)
Now, k = Area of circle / Area of equilateral triangle
Part 3 of the square-circle-triangle trilogy
The last puzzle of the set of 3 square-circle-triangle puzzles! (: Unfortunately you won't see much of the trio in future puzzles anymore!
Inscribed in a square is a circle, as shown below:

Suppose an equilateral triangle is fitted into one of the space bounded by the circumference of the circle and the sides of the square, such that one vertice of the triangle touches a corner of the square, and the other vertice just touches the circumference of the circle. (Diagram above)
Now, k = Area of circle / Area of equilateral triangle
Find, to the nearest integer, the value of k.
If you know the answer, post it in the comments section of this post.
If you know the answer, post it in the comments section of this post.

4 Comments:
At Sunday, October 01, 2006 3:28:00 PM, Anonymous said…
Anonymous said…
39
At Tuesday, October 03, 2006 6:58:00 PM, chorkie said…
chorkie said…
your answer is close, but incorrect.
At Tuesday, October 03, 2006 8:36:00 PM, Anonymous said…
Anonymous said…
38
At Tuesday, October 03, 2006 10:50:00 PM, chorkie said…
chorkie said…
yep u r right! (:
Post a Comment
<< Home